出品:新浪科技《科学大家》、高山大学
主讲嘉宾:夏志宏 高山大学教务长、校董,数学家、天文学家,美国西北大学终身教授
一、上帝玩掷骰子吗?
科学界经常会有这样的讨论:世界是确定的还是随机的?
爱因斯坦曾说过“上帝不跟宇宙玩掷骰子”。这句话是针对一些不太直观的量子力学理论的质疑。量子力学的基本思想与我们的直观感觉是完全不一样的,它认为在亚原子世界中所有的东西都是随机的,而且是真正的随机。有两个最著名的例子:“海森堡的测不准原理”和“薛定谔的猫”。
“海森堡的测不准原理”说的是,如果要准确测量原子的位置,那么就无法准确测量它的动量。这两个量没有办法同时准确测量。
“薛定谔的猫”是把微观世界和量子世界的东西扩展到宏观世界所做的生动描述。
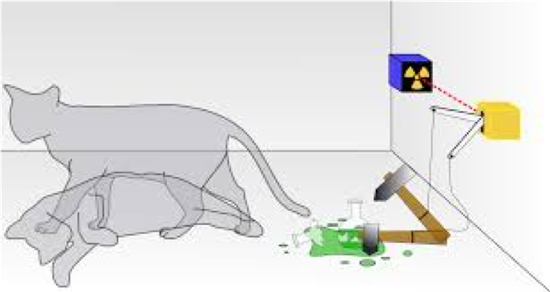 薛定谔的猫思想实验,图自维基百科
薛定谔的猫思想实验,图自维基百科薛定谔的猫:在一个盒子中放一只猫,这只猫的生死取决于某个原子的衰变。假如该原子发生了衰变,盒子中的毒气瓶就会被打破,释放出毒气,猫被毒死;假如该原子没有发生衰变,毒气瓶就不会被打破,猫不会被毒死。
原子的衰变是随机的。盒子打开之前,我们不知道猫是生还是死;盒子打开之后,就可以看到猫是活着的还是死了。盒子打开之前,一般人会认为猫的生死状态已经确定,只是我们不知道而已。
但量子力学并不这么认为。原子的衰变是以一定概率发生的,它有可能衰变也有可能不衰变。但在我们没有打开盒子之前,衰变的状态,我们当然是不知道。
但事实上不仅如此:并不是我们不知道,而是在我们观测之前,它本身就处于一个叠加的状态,衰变与否同时存在!
反映到宏观世界,在我们打开盒子之前,猫的“生”态和“死”态是叠加在一起的,“生”态和“死”态同时发生,在我们打开盒子的那一刻,“生”态或“死”态才得以确定。
这可能非常难以想象,也是为什么爱因斯坦当初会说“上帝不跟宇宙玩掷骰子”这句话。从此以后对“世界是随机的还是确定的”有了很多争论。
二、随机与确定的数学原理
从数学的角度来看,世界是随机的还是确定的,其实都是一回事,看似对立实则统一。
第一,随机系统并非随意,而是具有很强的确定性。
例如,对于房间中的空气,每一个空气分子都是随机的,但整体是一个非常确定的系统。
从数学上来讲,由于分子数量极大,可以应用大数定理和中心极限定理。这两个定理保证了在大数据情况之下,世界其实是确定的。
再例如,量子计算机利用的就是像薛定谔的猫一样的叠加态。它的每一个计算过程都是随机的,得到的可以说是一个随机结果,但在大量重复计算以后,就变成一个非常确定的结果。
第二,确定的系统有很强的随机性。
一个系统即使是完全由物理规律确定好的,它也会展现出非常随机的一面。最著名的例子就是“蝴蝶效应”。
对应于确定系统中出现的随机现象,数学中有一套理论叫做“混沌”,即动力系统的混沌理论。
用古人的说法,原因在于“差若毫厘,谬以千里”这样的哲学思想。我们由此可以得到宏观的世界也是测不准的原理,尽管它是一个确定系统。同样地,我们还可以确定将来是不可测的,其原因是混沌效应的存在。
三、随机系统的确定性
抛硬币的学问
我们先看一个简单的例子,抛硬币。
一枚硬币只有两面,正面与反面。抛出一枚硬币后出现的有可能是正面,也有可能是反面。一般情况下,出现正面和出现反面的概率是一样的,都是50%,除非硬币是特制的。
假设老师在概率课上布置作业,要求学生课后抛200次硬币,并把结果记录下来。下面是小张的记录,其中0代表硬币正面,1代表硬币反面。

小张的这个数据记录有非常大的可能性是在造假!也就是说他根本没有去抛硬币,而是随意写出了这串数字。
为什么认为小张是在做假呢?可以用最简单的办法来分析:数一下这个记录中0和1出现的次数。
我们发现这串数字有111个0,89个1,也就是说小张200次抛硬币的结果中有111次出现正面,89次出现反面。计算一下就会知道,这个结果的可信度非常低,低于1%,也就是说可能性不大。
抛硬币得到任何一串0、1数字都是有可能的,但是有些数字串出现的可能性非常小。
比如抛200次,每一次出现的都是0,或者每一次出现的都是1,这种情况基本上是不可能的。全是0或全是1的记录基本上可以肯定是造假的。
我们再看看小李的记录:

几乎可以肯定,小李也在造假。我们首先来数一下小李这个记录中0和1的个数:101个0,99个1。好像一点问题都没有,正面和反面出现的概率差不多。但是,我们发现在这个记录中,111出现了三次,而1111一次都没有出现。
我们可以去计算一下,抛200次硬币的过程中,出现111的次数小于或等于3的情形的可信度非常低,低于千分之一;一次1111都没有出现的可信度低于百分之一。所以,几乎可以肯定小李的记录也是随便做出来的,尽管他把0和1的概率设置得差不多,但其它方面还是存在问题。
也许有人可以伪造一些记录出来,把111和1111出现的频率也进行适当调整。但是在200个数字里面,不仅是111和1111,我们还可以再看010出现的次数,或者101出现的次数,这些都是有规律的。
我们看到,假如不真正去抛硬币而是想伪造出抛硬币的结果,这其实是非常难的。最简单的方法就是老老实实地去抛硬币,然后把结果写出来,这个时候数据内在的统一性才会体现出来,不然很难做到。
如何用大数据发现论文造假
我们经常会看到科学文献里有一大堆的数据,其中不乏数据造假的情况。同样的道理,造假的时候没法做到数据的统一性。所以,我们可以用大数据来打假。
假如下面是一组从某实验室得来的数据,总共有40个数字:

我们可以发现:
(1)每个数都有7位数字,包括小数点后面的6位数字;最后一位数字为0的一个都没有。
从心理上分析,造假者为了把小数点后的每个数字都写出来,一般来说他放的0就会非常少。而一组真正从实验中得来的数据,40个数字中一个0都没有的概率是非常小的。
(2)倒数第二位没有一个1。
这种情形出现的概率也是非常非常小的。一般的物理数据或任何通过实验得到的数据,精确的有效数字可能只有前面两三位数字。
在一些比较精确的实验中,可能有效数字更多,而其他一些实验里的有效数字比较少。假如说上面的例子中有效数字是三位,其后面几位数字基本上是随机的;即使有效数字是四位,那最后面的三位数字也是比较随机的。
一般的实验数据,最后几位数字都是比较随机的。所以,最后一位数不出现0的概率就非常小。我们可以用这种方法去找有可能做假的文章来进行打假分析,且数据量越大,打假就越精确。
我们也可以用一些更简单的办法。刚才这组数据总共才40个数字,这个数据量是比较小的,统计规律有时候不是那么明显。但我们可以不按照0、1、2、3、4、5、6、7、8、9来分,而是分成奇数和偶数两大类,这个时候它的统计规律会比较明显。或者可以把数据用二进制表示,此时某一位置上数字的统计规律就会体现得非常强。
随机系统的应用
我们可以利用随机系统的性质做一些真正有意义的统计。
例如,某个防疫部门需要以问卷形式统计某个传染病的发病情况,比如性病、肺结核等。
但出于对自己隐私的保护,调查对象可能不愿意对问卷上的有关问题进行如实回答,即使调查结果不会对外公布。
那该如何完成这项调查呢?
利用随机的性质,我们有一个简单的解决办法。给每个调查对象一个骰子,在回答问卷前自己投骰子,如果骰子出现的结果是1、2、3、4,就如实回答;如果骰子出现的结果是5、6,就一定要撒谎。
由于收问卷者并不知道每个人投骰子的具体情况,他也就不知道问卷上的答案是真是假。被调查者因此也可以毫无顾虑地回答问卷。
此时,尽管每个人的回答都是随机的,但按照前面讲的原理,整体的统计数据可以非常精确。
假设3万份问卷里有1.2万人回答有传染病,那么真实情况下应该是多少人?误差会有多大?
我们不妨来计算一下:假如真实情况下有病的人数为x,假定精确地有2/3如实回答,1/3撒谎,则回答有病的人应该是:
x∗2/3+(30000-x)∗1/3=12000
解这个方程可以得到x=6000。
由于每一次投骰子是一个随机的过程,所以有病的人数不一定是精确的6000人。假如置信区间放在95%,那么我们算出,这个统计结果的误差上下不超过139人,即真正有病的人数范围为6000±139;把置信区间放大到99%,最大的可能的误差也就是200人左右,所以统计结果还是相当可信的。
大数定理与中心极限定理
从上面的例子我们可以看出,随机系统中存在的确定性比想象的要强得多。在物质世界中,每个原子、分子都有很大的不确定性,但是把大量的原子、分子放在一起,这种不确定性就会消失,展示出非常强的确定性。
比如说抛100万次硬币,在置信度为0.26%(即±3δ)的情况下,正反面出现次数的平均值误差不会超过0.015。
有一些数学理论揭示了随机系统的一些非常好的内在规律,而其中最好的也是最简单的一个是大数定理。
大数定理告诉我们,一个实验重复次数多了,或者数据量大了以后,数据的平均值将会越来越接近数据的期望值。
中心极限定理是比大数定理更加精确的一个数学理论。它在形式上比大数定理要稍微复杂一点,但其实也很简单。
我们仍然考虑抛硬币的例子。假设正反面出现的概率各是50%,正面记录为0,反面记录为1。
 扔硬币概率分布1
扔硬币概率分布1扔第1次,记录为0的概率是50%,为1的概率也是50%;[见图(1)]
扔第2次,记录为0的概率是50%,为1的概率是50%;对前两次结果取平均,平均值为0的概率是25%,为1的概率是25%,另外还有50% 的概率为 0.5。[见图(2)]
扔第3次,对三次结果取平均,平均值为0(即记录为000)或平均值为1(即记录为111)的概率都很小。[见图(3)]
……
扔100次取平均,平均值的分布是中间突出,两边特别小,一百次全是0或全是1都基本上不可能。[见图(4)]
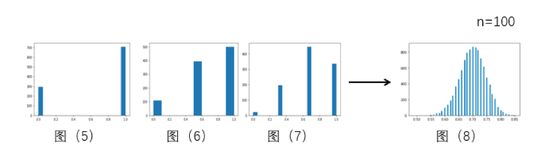 扔硬币概率分布2
扔硬币概率分布2如果我们换一个重量分布不均的硬币(一头重一头轻),其正反面出现的概率是不一样的。有趣的是,用这个非均匀硬币抛100次所得平均值的概率分布图形与之前抛均匀硬币100次所得到的概率分布图形在形状上几乎是一样的[图(4)与图(8)],都很像教堂里的钟。
中心极限定理是说,不管原来的概率分布是怎么样的,只要满足一些基本的性质要求,一次次重复实验,最后的平均值都呈现出钟形的分布。
四、确定系统的随机性
与随机系统相对应的是确定系统。一个确定系统的“确定性”并不是绝对的,有很多时候其实是不可测的。
故事:棋盘上的麦粒
 棋盘上的麦粒
棋盘上的麦粒传说一位印度的数学家发明了国际象棋,皇帝知道后很高兴,希望可以奖赏数学家。数学家说:“我要的不多,你在我棋盘的第1格放1颗麦子,第2格放2颗,第3格放4颗,第4格放8颗……用这种方式把棋盘放满了,我就满意了。”
皇帝一听,觉得数学家不是很贪婪,就要几颗麦子而已。但他没有想到的是,他得有多少麦子才能满足数学家的要求。我们可以简单算一下麦子的颗数:
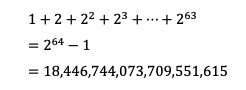
最后得到的是一个非常大的数字。可以简单换算一下,这么多颗麦子大概有140万亿升,约为去年全世界麦子产量的400倍。相当于将2000年以来全世界麦子的总产量放在棋盘上,才差不多满足数学家的要求。
这个例子说明,几何级数增长得特别快。开始看上去微不足道,但每一次增加的量大于以前所有量的总和。即使几何级数以7%的增速(比如我国的GDP),大概10年就会加倍。如果保持7%的增速,每十年的产值将会大于历史产值总和!
将来不可预测的混沌系统
假设一个封闭盒子里面装满了气体。我们可以数学证明气体分子在盒子里运动具有这样的性质:某一个气体分子的运动可能因为某些原因产生一个小的偏差,这个小的偏差将可能以指数形式增加,也就是每隔一段时间偏差会加倍。
由于气体分子运动比较快,它运动轨迹的误差可能不到一两秒钟就会加倍。假如是1秒钟加倍,64秒钟之后,这个误差就有可能超过“棋盘上的麦粒”那个故事中的天文数字。但是好在盒子对它的运动是有限制的,总体误差限制在盒子的范围之内。
从数学理论上来讲,假如系统存在这种机制,即在微观状态下误差呈指数增长,那么其影响的效果就要“差若毫厘,谬以千里”。指数增长是一种非常可怕的增长态势。存在这种增长机制的系统称为一个混沌动力系统。
在微观状态下,混沌动力系统的误差将按指数级增长。在宏观状态下,我们不知道它会怎么样,可能会因为运动的折返或者有其他宏观上的物理限制,使误差不会无止境地增长下去。
混沌的状态一般还可以量化,量化的结果在数学里面就是Lyapunov指数。Lyapunov指数是告诉我们微小误差经过多长时间加倍。假如每隔单位时间加倍的话,这个指数为ln(2)。假如每隔T单位时间加倍,这个指数就是ln(2)/T。
一个复杂系统的不同区域可能有不同的压缩指数。对于混沌的系统,结论是它的将来是不可预测的。最典型的“将来不可预测”的例子是蝴蝶效应。蝴蝶效应是气象系统的例子,指的是蝴蝶翅膀的微小抖动可以在几周的时间内引起全球性的气候变化。气象系统是非常复杂的混沌系统。
Lorenz 吸引子
Lorenz(洛伦茨)是麻省理工学院(MIT)的教授,他专门研究气象。气象方程是非常复杂的偏微分方程组,其解的结构非常复杂,有众多的未解问题。未来研究气象方程,Lorenz将其简化为一组三维空间的常微分方程:
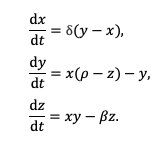
这个常微分方程里有三个参数δ、β和ρ,它看起来是一个非常简单的三维方程,但它有两个非线性项。一般来说,只要有非线性项的存在,基本上就不太可能用理论上的公式来精确求解,获取具体轨道,唯一的办法是采用数值计算。
当δ=10、β=8/3和ρ=28时,数值计算发现方程解的轨道呈现出下面的奇怪现象:
 奇异吸引子
奇异吸引子无论从哪里出发,所有轨道最终都会跑向以上这个图形,在数学上被称为一个奇异吸引子。
也就是说对于上面的三维方程,从几乎所有的初始点出发,跟踪该点的轨道就会发现,它在做一种非常类似的、看似简单的运动,其运动轨迹最终都会画出如上奇异吸引子的形状。
这个形状大致可分为两个部分,暂且定为左边和右边。但对每一根轨道的每一个时刻,运动出现在左边还是右边是非常随机的,看上去毫无章法。
在吸引子上任意选取一点,它的轨道往往在左边走若干圈后,再到右边走若干圈,然后再回到左边走若干圈,如此往返,以至无穷。
每一次在每一边走的圈数由初始点决定,类似于蝴蝶效应,稍微变动一下初始点位置,但一定时间以后就会出现很大差异,将来出现在左边和右边的次数就与原来完全不一样。也就是说,长时间以后,出现在左边或右边变成完全随机。
Lorenz系统是一个混沌系统。它是一个确定性的动力系统,因为它的运动完全由一组常微分方程确定;但是它具有不可测性,即我们没有任何办法去精确地知道一个点经过长时间运动后的位置。只要时间长了,一个非常小的误差都会给最终测量带来非常大的、不可接受的误差。
五、复杂度、信息量和熵
如果把Lorenz系统的运动轨道按出现在左边或右边分别标记为0或1,我们就会发现对于这样一个确定的动力系统,它的运动轨道也与前面一串抛硬币的实验结果一样,可以得到一串由0和1组成的数字序列。在信息学领域,一串摩尔斯密码也给出了一串由0和1组成的序列。
Lorenz系统、抛硬币实验、摩尔斯密码,这三个例子分别代表了确定系统、随机系统和信息传播系统。而从数学的角度来看,它们是一模一样的,没有任何区别。
一根轨道、一串抛硬币实验和一串摩尔斯密码带来的都是一串0或1的字符。所以,这三个系统在本质上不存在所谓的随机和确定的严格区分,而且它们的很多性质可以用同一种方法去研究,比如我可以研究不同系统的复杂性。
熵的概念是度量动力系统复杂性的一种方式,熵越大表示系统越复杂。但在概率论和信息学里同样的概念,或者同样的量,有不同的意义和应用。
熵在概率学或信息论里代表的是信息量,或者说是信息量的期望值。熵越大则信息量越高。信息量在大数据分析里有重要的应用。
熵在网络或信息传播学里代表的是网络容量和传播能力。熵越大则网络容量越大。
综上所述,表面上看这些系统以及相对应的概念是完全不一样的,有时甚至是相对立的,比如说随机和确定的系统,但数学把他们巧妙地统一起来了。
随机?确定?这取决于你观察的位置。
本文根据夏志宏教授2020年3月21日在高山大学和更新学堂联合出品的“科学公益直播”的课程整理而成,经老师审核后公开发布。
推荐
《科学大家》专栏投稿邮箱:sciencetougao@sina.com 来稿请注明姓名、单位、职务



“掌”握科技鲜闻 (微信搜索techsina或扫描左侧二维码关注)




![[思考] [思考]](https://n.sinaimg.cn/commnet/2018new_sikao_org.png)