文/马让平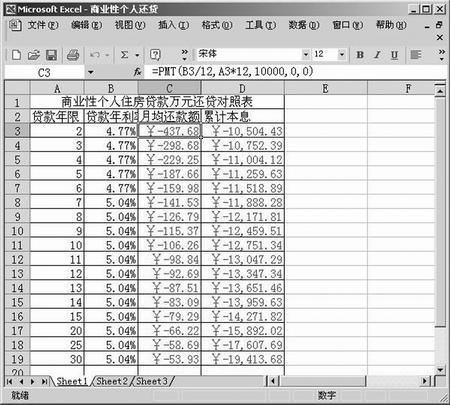

图1

　　俗语说：不算计，一生穷.现代家庭，手捧一份收入，总要考虑将它运用到何处，收益才最大。比如买保险，分期付款买车、买房、买债券之类的。要计算合不合算，比较复杂。这次我们来学习几个函数，看看它们在居家理财方面给我们带来的帮助。

　　注意：如果下述函数不可用，并返回错误#NAME?，请安装并加载“分析工具库”加载宏。

　　一、分期付款的计算

　　我们现在买房一般是用分期付款的方式。下面介绍的几个函数就是用来计算每期的付款额，让我们对将来的还贷计划做到心中有数，量入为出。

　　1.IPMT(r,p,n,pv,fv,t)函数用来计算在某一给定期次内的利息偿还额。

　　2.PPMT(r,p,n,pv,fv,t)函数用来计算在某一给定期次内的本金偿还额。

　　3.PMT(r,n,pv,fv,t)函数用来计算每期付款额(包含本金和利息)。

　　以上函数内部参数含义为：“r”为利率;“p”为计算要偿还利息(本金)数额的期数，必须在1到n之间; n为付款期总数；“pv”为现值(或本金)；“fv”为未来值或在最后一次支付后希望得到的现金余额；“t”用以指定各期的付款时间是在期初还是期末。0表示期末，1表示期初。

　　我们以一笔住房抵押贷款为例说明它的用法：年利率5.04%;期限10年；贷款额10万元。那么在等额分期付款方式下，该怎么付款呢？

　　分析：该笔贷款在第一个月要偿还的利息为:IPMT(5.04%/12,1,120,100000,0,0)=-420元

　　该笔贷款在第一个月要偿还的本金为:PPMT(5.04%/12,1,120,100000,0,0)=-642.61元

　　该笔贷款在每个月要偿还的本金和利息为:PMT(5.04%/12,120,100000,0,0)=-1062.61元

　　因此利用PMT(r,n,pv,fv,t)函数完全可以编制一张在不同期限,不同利率下的分期付款还贷对比表,以助我们选择最佳的贷款方式。如表一所示：

　　(图表一说明：“月均还款额”列用的就是PMT(r,n,pv,fv,t)函数，“累计本息”列用的是以下公式：=“月均还款额”ד贷款年限”×12)

　　二、PV(r,n,pw,fv,t)函数

　　该函数返回某项投资的现值。(有关现值,终值,年金现值,年金终值的含义请参阅有关财务管理方面的书籍)参数r,n,fv,t的含义同上；参数pw为各期应付出或得到的款项,其数值在整个投资期内保持不变。

　　我们还是用实例来说话吧。

　　例1.某人想购买一项保险年金,现在只需一次支付12万元。该保险可以在今后12年内每年回报2万元，假定投资回报率为14%，买不买？

　　分析：从表面上看12×20000=240000元，远大于原始投资额120000元，应当购买。其实不然，12年后得到的收益与现在的投入不是在同一时点上，不能直接比较。(想想,今天的1元和2年后的1元是不是等值呢？)所以要将以后的总收入折算成现值，才好和现在的投资额相比。

　　12年的总收益折算的现值=PV(14%,12,20000,0,0)=-113205.84元,小于目前付出的12万元,故不应当购买此项保险.

　　例2.某人希望在5年后有10万元好购入一部新车，若年利率为5%，则现在他需要一次性存入银行多少钱。

　　分析:该人现在需存入的钱：PV(5%,5,0,100000,0)=-78352.62元

　　(注意例1和例2是有区别的)

　　三、FV(r,n,pw,pv,t)函数

　　该函数返回某项投资的终值(未来值)。该函数参数的含义可参阅前面所述.

　　例1.某人准备在今后20年内，每月末从收入中提取400元存入银行，以备将来小孩上学所需。若以年息5%计算，问20年后可积累多少钱。

　　分析：20年后价值=FV(5%/12,240,400,0,0)=164413.47元

　　例2.某人将15000元存入银行，以备5年后另作他用。若以年息5%计算，则5年后有多少钱。

　　分析：5年后的价值:FV(5%,5,0,15000,0)=19144.22元

　　(注意例1和例2是有区别的)